Segunda parte sobre cores e o tal Gamut multidimensional

Beleza, na última postagem tetamos entender melhor o que é exatamente uma cor fundamental, de onde elas vem e o que comem. Basicamente relembramos que as cores são frequências distintas de oscilação da luz e que o espectro do visível contém todas as frequências da luz visível. Porém ele não contém todas as cores que percebemos, pois, como notas musicais, uma cor pode ser composta de diversas frequências misturadas em padrões complexos.

De fato, o espectro do visível pode ser representado facilmente em uma reta que muda de cor continuamente, começando no violeta e acabando no vermelho, como na imagem abaixo:

Cada faixa vertical dele corresponde a uma frequência de vibração específica da luz, e essa frequência pode variar continuamente desde o valor mais baixo no vermelho (400 Thz) até o valor mais alto no violeta (789 Thz), e cada frequência (mesmo fracionária) corresponderá a uma cor. Dizemos que esse espectro possui somente uma dimensão pois qualquer cor nele pode ser descrita por apenas uma coordenada, o valor de sua frequência. Não somente isso, mas ele é linear, a soma de uma frequência com outra resulta numa soma linear (400+200=600 por exemplo). Aqui precisamos citar que apesar desse espectro ser linear, nossa percepção de cores não é, o que vai gerar futuramente diversos problemas. Quer dizer, se você duplica a frequência, o resultado é (como esperado) duas vezes a frequência.

Porém para nossa percepção, as coisas são muito mais complexas. Por exemplo, a diferença de frequências entre laranja e vermelho é quase a mesma diferença do azul para o índigo. Mas enquanto quase todas as pessoas sabem facilmente diferenciar vermelho de laranja, poucos conseguem dizer com certeza se algo é azul ou índigo. Ou seja, enquanto usar um espectro baseado nas frequências é útil para ajustar as cores de maneira linear, baseadas em suas frequências, em termos práticos isso pode ser muito ruim, já que não percebemos as diferenças entre cores de maneira linear. Na verdade o olho humano é extremamente eficiente em diferenciar tons próximos do verde, enquanto tem dificuldades perto do azul. Isso se deve a diversos motivos evolutivos, mas é fácil entender que durante a evolução foi muito mais importante diferenciar certas core. Vermelho e amarelo por exemplo indicam veneno geralmente, e não podemos nos dar ao luxo de confundi-las com azul claro. Já a diferença entre índigo e azul não é exatamente algo de vital importância na selva, onde pouquíssimas coisas tem esses tons. A imagem abaixo mostra a sensibilidade média da população a diversas cores para exemplificar esse ponto.

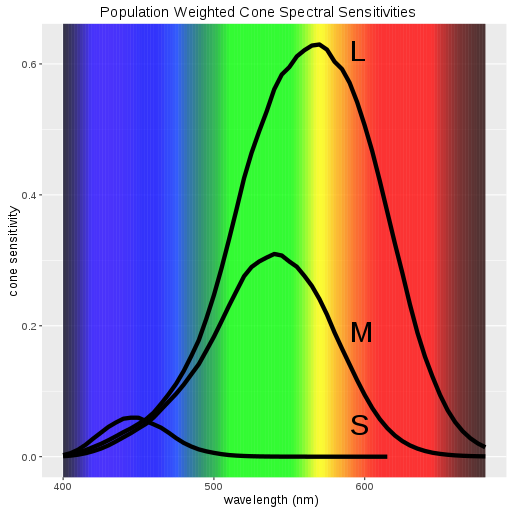
Ok, temos o espectro unidimensional de frequências, que contêm todas as frequências visíveis. Mas como discutimos na postagem anterior, onde está o cinza? O marrom? O rosa choque? Bem, como uma nota de violino tem seu próprio timbre, o que nós percebemos como cores na verdade são misturas de diversas frequências entrelaçadas e com padrões bem específicos. E essas cores não estão contidas no espectro clássico e linear.

Podemos pensar inicialmente nessas cores citadas como sendo as mesmas frequências do espectro linear mas com uma intensidade muito maior ou muito menor, seu “brilho”. Assim, o ciano seria uma frequência de azul específica e com muito brilho, enquanto azul da Prússia seria outro tom de azul com menor brilho. E desse modo conseguimos também os tons de cinza que queríamos, ficando nos extremos entre preto e branco. Mas essas cores todas não poderiam ser “espremidas” no espectro linear que já construímos. Afinal, não estamos mudando a frequência de nenhuma delas, somente a intensidade da luz, sua “potência”.  Para que nós possamos adicioná-las vamos precisar de uma dimensão a mais. Teremos um “plano” de cores, onde o eixo horizontal é a frequência e o eixo vertical é a “intensidade” de cada cor:

Hummm as coisas estão ficando mais interessantes. Para definir uma cor nesse plano eu preciso agora de duas coordenadas, a frequência (valor horizontal) e a intensidade (valor vertical). E como dissemos antes, no extremo de baixa intensidade temos o preto, independente da frequência, enquanto para a intensidade máxima (no topo) temos o branco, também independente da frequência. Agora vemos muito mais cores do que no espectro clássico, super simplificado e unidimensional. Note que nessa representação tanto a frequência das cores (eixo horizontal “x”) quanto a intensidade (eixo vertical “y”) são ainda sim lineares. Para fins didáticos nós iremos continuar usando a representação de cores lineares acima. Mas como dissemos antes, a nossa percepção psicológica das cores não é linear nas frequências, e supervalorizamos alguns tons mais que outros. Para resolver esse “problema” existem diversas representações e métricas que distorcem o espaço bidimensional, dando mais espaço a tons que nós percebemos melhor. Esse é o caso de uma das representações mais usadas em pesquisas quanto a cores, o espaço de cores CIE 1931:

Note que diferente do nosso quadrado anterior, agora a “paleta” de tons verdes é muito maior, e se quisermos variar a frequência de uma cor, agora precisamos andar pela borda da imagem, e não variar linearmente a escala horizontal. Essa métrica é muito útil quando se é um especialista em design de interiores e sua vida depende de escolher entre rosa-creme e fushicha. Como esse não é nosso caso, prosseguimos com a imagem das cores mapeadas em um plano bidimensional quadrado que havíamos mostrado. Nesse caso ainda sim faltam cores. Se você der scroll up e olhar bem, ainda sim não temos cores como o marrom ou rosa choque naquele quadrado. Isso fica mais evidente se comparamos com a imagem mostrada na postagem anterior do círculo de cores:

Essa imagem também é bidimensional, com a cor em sí variando com o ângulo (como os ponteiros de um relojo) e alguma outra característica variando com o raio, ou seja, a distância do centro. A primeira vista pode parecer que conforme chegamos perto do centro estamos aumentando a luminosidade da cor, pois parece cada vez mais branco a coisa. Mas estamos na verdade variando ainda outra característica da cor, sua saturação. Conforme caminhamos para o centro do círculo (diminuindo a coordenada “distancia do centro” ou seja “raio”) vemos que as cores vão ficando mais “lavadas”, sem a saturação de sua cor original. Isso é diferente de aumentarmos ou diminuirmos seu brilho, sua intensidade. Então aqui temos ainda outra característica que pode ser variada independentemente das outras.

Se combinarmos as três características, enfim, poderemos ter uma representação minimamente digna da maioria das cores perceptíveis. Relembrando, temos então a cor em si, que corresponde a sua frequência original (azul por exemplo), e que pode variar continuamente, mudando assim a tonalidade. Temos a intensidade da cor, que corresponde a grosso modo a sua iluminação, ou brilho. Essa também pode variar continuamente dentro de uma mesma cor, nos dando diversos sombreamentos da mesma cor (azul escuro, azul muito claro, etc). E por fim temos a saturação, que é o quanto a cor esta “lavada” ou o quanto ela parece desbotada por assim dizer. E variando essa característica temos variações ainda mais sutis dentro da mesma cor e da mesma intensidade. No quadrado bidimensional la de cima temos a frequência das cores no eixo “x” e a intensidade no eixo ‘y’ . Já no círculo acima temos a frequência da cor sendo variada conforme giramos no sentido horário (damos o nome disso de variável angular, pois para cada ângulo do círculo existirá uma cor) e a coordenada de distância do centro do círculo nos dá a saturação da cor. Vamos combinar isso em três dimensões.

Imagine que temos um desses círculos de cores. Ele possui uma intensidade bem definida, que é a mesma para todas as cores contidas nele. Agora imagine outro desses discos, mas com a intensidade levemente reduzida, onde todas as cores ficaram mais escuras.  Empilhamos um logo abaixo do outro. E então colocamos outro ainda mais escuro ligeiramente abaixo desse. E assim por diante. No fim acabamos com um gigantesco cilindro, em que a intensidade das cores vai variar com a altura. Percorrendo o cilindro no sentido horário ou anti-horário em qualquer altura podemos ver cores diferentes. E nos aproximando do centro podemos mudar a saturação de cada cor em cada intensidade específica! O resultado final é o modelo HSV abaixo (que foi fatiado ao meio para podermos ver o “interior”):

O “valor”, no eixo vertical, é a intensidade da cor (e fisicamente corresponde a amplitude total das frequências emitidas). Se giramos a roda angularmente, mudamos a frequência principal, e portanto a “cor” em si (o hue). E por fim, nos afastando do eixo central do cilindro, vamos aumentando cada vez mais a saturação (o que fisicamente corresponde a diminuirmos o desvio da gausseana, quanto maior a saturação, mais a intensidade ficará com um pico bem definido em somente uma frequência. Quanto menor a saturação, mais “gorda” a gausseana, com diversas frequências se misturando.) Note que agora temos uma fração bem maior das cores que percebemos, incluindo todos os tons de cinza, que ficam justamente no eixo central do cilindro (raio zero) começando no preto bem no fundo e chegando ao branco no topo.

Evidentemente essa é uma, de várias, representações para as cores. Devido às cores com valor 0  representarem o preto independente do Hue ou da saturação (chroma), esse diagrama também pode ser desenhado como um cone, onde se o valor é zero, você não pode variar o raio (ja que tudo seria preto). Claro que o cone também cresce para cima, com o valor aumentando cada vez mais até o branco mais intenso.

Outra representação muito usada em programas de computador é o RGB, nesse caso o cubo RGB usa cada eixo (X, Y e Z) como coordenada para indicar a quantidade de cor vermelho (R) verde (G) e azul (B) de cada cor, gerando uma organização totalmente diferente das cores, como abaixo:

Note no entanto que tal organização não é muito eficiente no sentido de que ela é linear nas diferenças das cores, e como comentamos anteriormente, a percepção humana valoriza mais alguns tons de cores em detrimento a outros. Não somente isso, mas o modelo de cores RGB define quantidades absolutas de “vermelho”, “azul” ou “verde”, e isso é problemático pois uma tela de cristal líquido pode ter uma intensidade máxima de verde muito diferente de uma tela antiga de tubo. Isso gera inconsistências grandes nesse modelo, onde uma coordenada gera cores diferentes dependendo se você está vendo a cor na tela do celular, imprimindo numa impressora a laser ou vendo a imagem na tela de uma TV de plasma.

Para criar um espaço de cores que não dependa de dispositivos, e que a diferença de espaço entre cores próximas seja equivalente a diferença que nosso olho percebe, existem alguns modelos, sendo que um famoso é o SCILAB. Nele as cores são dispostas também em três dimensões, porém uma dessas dimensões é a intensidade, e as outras duas restantes são a quantidade de cores “opostas”, no caso o eixo x tem o verde em uma ponta e o vermelho em outra, e no eixo y temos o amarelo numa ponta e o azul em outra. Não somente isso, mas a métrica do espaço é deformada para que as cores estejam nas distâncias correspondentes a nossa percepção, gerando uma forma tridimensional no mínimo curiosa:

Todos esses são sistemas de organização de cores, alguns são melhores para o uso em softwares, outros em sistemas de impressão, outros para classificações de cores a nível de estudos de percepção. No fim a questão que importa é que eles são complementares, e não existe um sistema “melhor” que o outro em todos os níveis, do mesmo jeito que não existem 3 cores mais “fundamentais” que outras do ponto de vista físico, apesar de isso fazer sentido quando você quer criar pigmentos a partir de aquarela ou guache.

Mas a parte mais importante é mais sutil: dimensões. Nós vimos como o espectro de cores tradicional tem somente uma dimensão (a frequência da cor). Conseguimos adicionar outra dimensão nele ao usarmos uma característica que seja totalmente independente da primeira (intensidade da cor), obtendo um plano de cores. Ao encontrarmos uma terceira característica que fosse independente das duas primeiras (a saturação) conseguimos adicionar ainda sim uma terceira dimensão à nossa escala de cores! Montamos a partir de disso um espaço tridimensional que não tem  nada a ver com as dimensões espaciais clássicas de largura/profundidade/altura. E é exatamente notando tais propriedades independentes que conseguimos montar espaços com ainda mais dimensões, e mais importante ainda, visualiza-los (mesmo que em partes)!